Abstract
The phenomenon of ‘‘rule learning’’—quick learning of abstract regularities from exposure to a limited set of stimuli—has become an important model system for understanding generalization in infancy. Experiments with adults and children have revealed differences in performance across domains and types of rules. To understand the representational and inferential assumptions necessary to capture this broad set of results, we introduce three ideal observer models for rule learning. Each model builds on the next, allowing us to test the consequences of individual assumptions. Model 1 learns a single rule, Model 2 learns a single rule from noisy input, and Model 3 learns multiple rules from noisy input

Introduction:

1. Introduction: from ‘‘rules vs. statistics’’ to statistics over rules
A central debate in the study of language acquisition concerns the mechanisms by which human infants learn the structure of their first language. Are structural aspects of language learned using constrained, domain-specific mechanisms (Chomsky, 1981; Pinker, 1991), or is this learning accomplished using more general mechanisms of statistical inference (Elman et al., 1996; Tomasello, 2003)?
Subsequent studies of rule learning in language acquisition have addressed all of these questions, but for the most part have collapsed them into a single dichotomy of ‘‘rules vs. statistics’’ (Seidenberg & Elman, 1999). The poles of ‘‘rules’’ and ‘‘statistics’’ are seen as accounts of both how infants represent their knowledge of language (in explicit symbolic ‘‘rules’’ or implicit ‘‘statistical’’ associations) as well as which inferential mechanisms are used to induce their knowledge from limited data (qualitative heuristic ‘‘rules’’ or quantitative ‘‘statistical’’ inference engines). Formal computational models have focused primarily on the ‘‘statistical’’ pole: for example, neural network models designed to show that the identity relationships present in ABA-type rules can be captured without explicit rules, as statistical associations between perceptual inputs across time (Altmann, 2002; Christiansen & Curtin, 1999; Dominey & Ramus, 2000; Marcus, 1999; Negishi, 1999; Shastri, 1999; Shultz, 1999, but c.f. Kuehne, Gentner, & Forbus, 2000).
We believe the simple ‘‘rules vs. statistics’’ debate in language acquisition needs to be expanded, or perhaps exploded. On empirical grounds, there is support for both the availability of rule-like representations and the ability of learners to perform statistical inferences over these representations. Abstract, rule-like representations are implied by findings that infants are able to recognize identity relationships (Tyrell, Stauffer, & Snowman, 1991; Tyrell, Zingaro, & Minard, 1993) and even newborns have differential brain responses to exact repetitions (Gervain, Macagno, Cogoi, Peña, & Mehler, 2008).
Learners are also able to make statistical inferences about which rule to learn. For example, infants may have a preference towards parsimony or specificity in deciding between competing generalizations: when presented with stimuli that were consistent with both an AAB rule and also a more specific rule, AA di (where the last syllable was constrained to be the syllable di), infants preferred the narrower generalization (Gerken, 2006, 2010). Following the Bayesian framework for generalization proposed by Tenenbaum and Griffiths (2001), Gerken suggests that these preferences can be characterized as the products of rational statistical inference.
On theoretical grounds, we see neither a pure ‘‘rules’’ position nor a pure ‘‘statistics’’ position as sustainable or satisfying. Without principled statistical inference mechanisms, the pure ‘‘rules’’ camp has difficulty explaining which rules are learned or why the right rules are learned from the observed data. Without explicit rule-based representations, the pure ‘‘statistics’’ camp has difficulty accounting for what is actually learned; the best neural network models of language have so far not come close to capturing the expressive compositional structure of language, which is why symbolic representations continue to be the basis for almost all state-of-the-art work in natural language processing (Chater & Manning, 2006; Manning & Schütze, 2000).
Driven by these empirical and theoretical considerations, our work here explores a proposal for how concepts of ‘‘rules’’ and ‘‘statistics’’ can interact more deeply in understanding the phenomena of ‘‘rule learning’’ in human language acquisition.
Our approach is to create computational models that perform statistical inference over rulebased representations and test these models on their fit to the broadest possible set of empirical results. The success of these models in capturing human performance across a wide range of experiments lends support to the idea that statistical inferences over rule-based representations may capture something important about what human learners are doing in these tasks.
Our models are ideal observer models: they provide a description of the learning problem and show what the correct inference would be, under a given set of assumptions. The ideal observer approach has a long history in the study of perception and is typically used for understanding the ways in which performance conforms to or deviates from the ideal (Geisler, 2003).
With few exceptions (Dawson & Gerken, 2009; Johnson et al., 2009), empirical work on rule learning has been geared towards showing what infants can do, rather than providing a detailed pattern of successes and failures across ages.

Models
The hypothesis space is constant across all three models, but the inference procedure varies depending on the assumptions of each model.
Our approach is to make the simplest possible assumptions about representational components, including the structure of the hypothesis space and the prior on hypotheses. As a consequence, the hypothesis space of our models is too simple to describe the structure of interesting phenomena in natural language, and our priors do not capture any of the representational biases that human learners may brings to language acquisition.
Nevertheless, our hope is that this approach will help in articulating the principles of generalization underlying experimental results on rule learning.
2.1. Hypothesis space
This hypothesis space is based on the idea of a rule as a restriction on strings. We define the set of strings S as the set of ordered triples of elements s1, s2, s3 where all s are members of vocabulary of elements, V. There are thus |V|3 possible elements in S.
For each set of simulations, we define S as the total set of string elements used in a particular experiment.
For example, in Marcus et al (1999): set of elements S = {ga, gi, ta, ti, na, ni, la, li}. These elements are treated by our models as unique identifiers that do not encode any information about phonetic relationships between syllables.
A rule defines a subset of S. Rules are written as ordered triples of primitive functions (f1, f2, f3). Each function operates over an element in the corresponding position in a string and returns a truth value. For example, f1 defines a restriction on the first string element, x1. The set F of functions is a set which for our simulations includes ^ (a function which is always true of any element) and a set of functions is y(x) which are only true if x = y where y is a particular element. The majority of the experiments addressed here make use of only one other function: the identity function =a which is true if x = xa. For example, in Marcus et al. (1999), learners heard strings like ga ti ti and ni la la, which are consistent with (^, ^, =2) (ABB, or ‘‘second and third elements equal’’). The stimuli in that experiment were also consistent with another regularity, however: (^,^,^), which is true of any string in S. One additional set of experiments makes use of musical stimuli for which the functions >a and <a (higher than and lower than) are defined. They are true when x > xa and x < xa respectively.

Model 1: single rule

Model 1 begins with the framework for generalization introduced by Tenenbaum and Griffiths (2001). It uses exact Bayesian inference to calculate the posterior probability of a particular rule r given the observed set of training sentences T = t1 . . . tm. This probability can be factored via Bayes’ rule into the product of the likelihood of the training data being generated by a particular rule p(T|r), and a prior probability of that rule p®, normalized by the sum of these over all rules:



We assume a uniform prior p® = 1/|R|, meaning that no rule is a priori more probable than any other. For human learners the prior over rules is almost certainly not uniform and could contain important biases about the kinds of structures that are used preferentially in human language (whether these biases are learned or innate, domaingeneral or domain-specific).
We assume that training examples are generated by sampling uniformly from the set of sentences that are congruent with one rule. This assumption is referred to as strong sampling, and leads to the size principle: the probability of a particular string being generated by a particular rule is inversely proportional to the total number of strings that are congruent with that rule (which we notate |r|).
Model 2: single rule under noise
Model 1 assumed that every data point must be accounted for by the learner’s hypothesis. However, there are many reasons this might not hold for human learners: the learner’s rules could permit exceptions, the data could be perceived noisily such that a training example might be lost or mis-heard, or data could be perceived correctly but not remembered at test. Model 2 attempts to account for these sources of uncertainty by consolidating them all within a single parameter. While future research will almost certainly differentiate these factors (for an example of this kind of work, see Frank, Goldwater, Griffiths, & Tenenbaum, 2010), here we consolidate them for simplicity.
To add noise to the input data, we add an additional step to the generative process: after strings are sampled from the set consistent with a particular rule, we flip a biased coin with weight a. With probability a, the string remains the same, while with probability 1 - a, the string is replaced with another randomly chosen element.
Under Model 1, a rule had likelihood zero if any string in the set T was inconsistent with it. With any appreciable level of input uncertainty, this likelihood function would result in nearly all rules having probability zero. To deal with this issue, we assume in Model 2 that learners know that their memory is fallible, and that strings may be misremembered with probability 1 - a.



Model 3: multiple rules under noise
Model 3 loosens an additional assumption: that all the strings in the input data are the product of a single rule. Instead, it considers the possibility that there are multiple rules, each consistent with a subset of the training data. We encode a weak bias to have fewer rules via a prior probability distribution that favors more compact partitions of the input. This prior is known as a Chinese Restaurant Process (CRP) prior (Rasmussen, 2000); it introduces a second free parameter, c, which controls the bias over clusterings. A low value of c encodes a bias that there are likely to be many small clusters, while a high value of c encodes a bias that there are likely to be a small number of large clusters. The joint probability of the training data T and a partition Z of those strings into rule clusters is given by P(T,Z) = P(T|Z)P(Z) neglecting the parameters a and c. The probability of a clustering P(Z) is given by CRP(Z,c).
Unlike in Models 1 and 2, inference by exact enumeration is not possible and so we are not able to compute the normalizing constant. But we are still able to compute the relative posterior probability of a partition of strings into clusters (and hence the posterior probability distribution over rules for that cluster). Thus, we can use a Markovchain Monte Carlo (MCMC) scheme to find the posterior distribution over partitions. In practice we use a Gibbs sampler, an MCMC method for drawing repeated samples from the posterior probability distribution via iteratively testing all possible cluster assignments for each string (MacKay, 2003).
In all simulations we calculate the posterior probability distribution over rules given the set of unique string types used in the experimental stimuli. We use types rather than rather than individual string tokens because a number of computational and experimental investigations have suggested that types rather than tokens may be a psychologically natural unit for generalization (Gerken & Bollt, 2008; Goldwater, Griffiths, & Johnson, 2006; Richtsmeier, Gerken, & Ohala, in press).
To assess the probability of a set of test items E = e1 . . . en (again computed over types rather than tokens) after a particular training sequence, we calculate the total probability that those items would be generated under a particular posterior distribution over hypotheses. This probability is



which is the product over examples of the probability of a particular example, summed across the posterior distribution over rules p(R|T). For Model 1 we compute p(ek|rj) using Eq. (2); for Models 2 and 3 we use Eq. (4). We use surprisal as our main measure linking posterior probabilities to the results of looking time studies. Surprisal (negative log probability) is an information-theoretic measure of how unlikely a particular outcome is. It has been used previously to model adult reaction time data in sentence processing tasks (Hale, 2001; Levy, 2008) as well as infant looking times (Frank, Goodman, & Tenenbaum, 2009).

Results

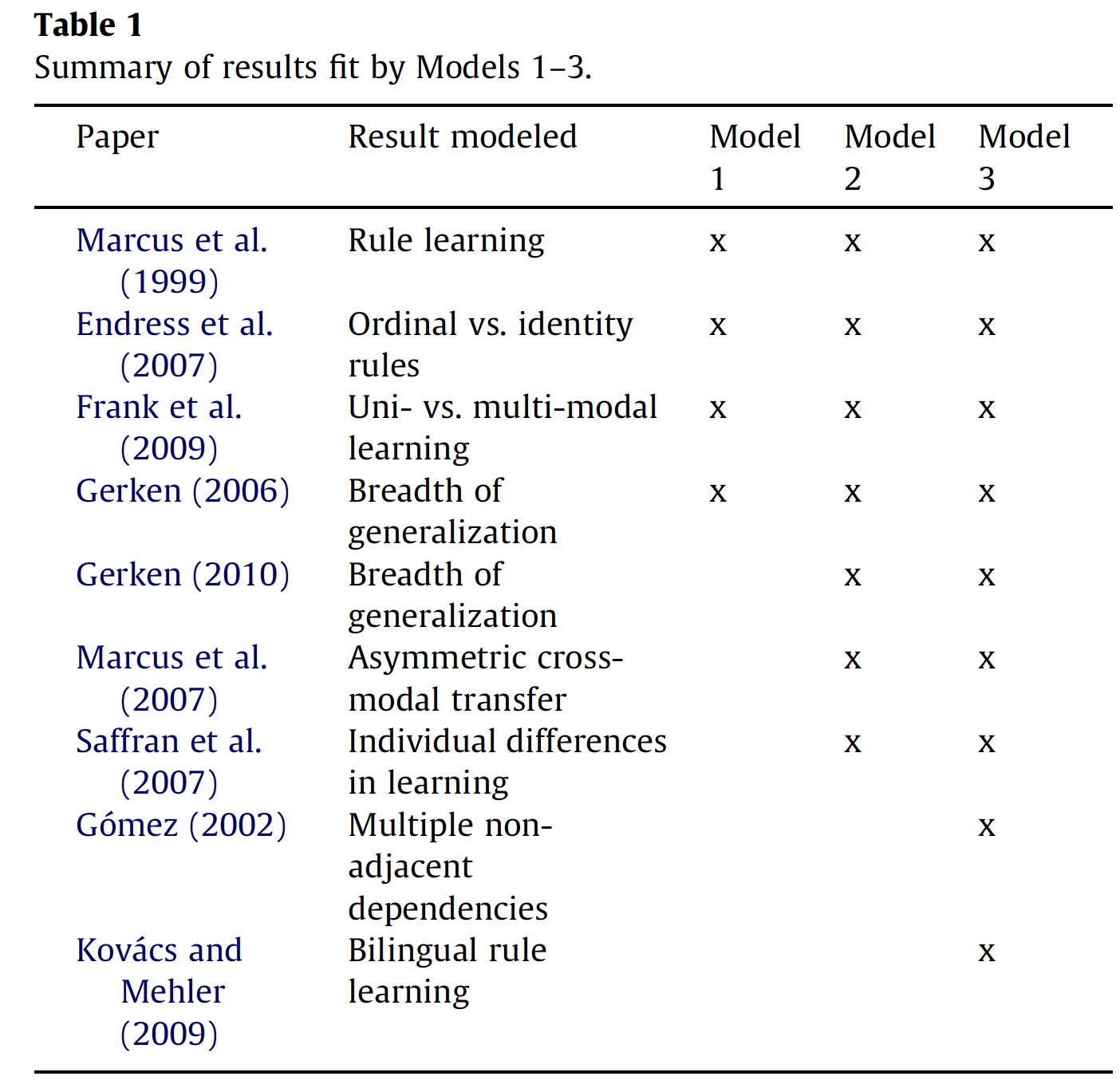
Conclusions:

The infant language learning literature has often been framed around the question ‘‘rules or statistics?’’ We suggest that this is the wrong question. Even if infants represent symbolic rules with relations like identity—and there is every reason to believe they do—there is still the question of how they learn these rules, and how they converge on the correct rule so quickly in a large hypothesis space. This challenge requires statistics for guiding generalization from sparse data.
from sparse data. In our work here we have shown how domain-general statistical inference principles operating over minimal rule-like representations can explain a broad set of results in the rule learning literature.
The inferential principles encoded in our models—the size principle (or in its more general form, Bayesian Occam’s razor) and the non-parametric tradeoff between complexity and fit to data encoded in the Chinese Restaurant Process—are not only useful in modeling rule learning within simple artificial languages. They are also the same principles that are used in computational systems for natural language processing that are engineered to scale to large datasets. These principle have been applied to tasks as varied as unsupervised word segmentation (Brent, 1999; Goldwater, Griffiths, & Johnson, 2009), morphology learning (Albright & Hayes, 2003; Goldwater et al., 2006; Goldsmith, 2001), and grammar induction (Bannard, Lieven, & Tomasello, 2009; Klein & Manning, 2005; Perfors, Tenenbaum, & Regier, 2006).
First, our models assumed the minimal machinery needed to capture a range of findings. Rather than making a realistic guess about the structure of the hypothesis space for rule learning, where evidence was limited we assumed the simplest possible structure. For example, although there is some evidence that infants may not always encode absolute positions (Lewkowicz & Berent, 2009), there have been few rule learning studies that go beyond three-element strings. We therefore defined our rules based on absolute positions in fixed-length strings. For the same reason, although previous work on adult concept learning has used infinitely expressive hypothesis spaces with prior distributions that penalize complexity (e.g. Goodman, Tenenbaum, Feldman, & Griffiths, 2008; Kemp, Goodman, & Tenenbaum, 2008), we chose a simple uniform prior over rules instead. With the collection of more data from infants, however, we expect that both more complex hypothesis spaces and priors that prefer simpler hypotheses will become necessary.
Second, our models operated over unique string types as input rather than individual tokens. This assumption highlights an issue in interpreting the a parameter of Models 2 and 3: there are likely different processes of forgetting that happen over types and tokens. While individual tokens are likely to be forgotten or misperceived with constant probability, the probability of a type being misremembered or corrupted will grow smaller as more tokens of that type are observed (Frank et al., 2010). An interacting issue concerns serial position effects. Depending on the location of identity regularities within sequences, rules vary in the ease with which they can be learned (Endress, Scholl, & Mehler, 2005; Johnson et al., 2009). Both of these sets of effects could likely be captured by a better understanding of how limits on memory interact with the principles underlying rule learning. Although a model that operates only over types may be appropriate for experiments in which each type is nearly always heard the same number of times, models that deal with linguistic data must include processes that operate over both types and tokens (Goldwater et al., 2006; Johnson, Griffiths, & Goldwater, 2007).
Finally, though the domain-general principles we have identified here do capture many results, there is some additional evidence for domain-specific effects. Learners may acquire expectations for the kinds of regularities that appear in domains like music compared with those that appear in speech (Dawson & Gerken, 2009); in addition, a number of papers have described a striking dissociation between the kinds of regularities that can be learned from vowels and those that can be learned from consonants (Bonatti, Peña, Nespor, & Mehler, 2005; Toro, Nespor, Mehler, & Bonatti, 2008). Both sets of results point to a need for a hierarchical approach to rule learning, in which knowledge of what kinds of regularities are possible in a domain can itself be learned from the evidence. Only through further empirical and computational work can we understand which of these effects can be explained through acquired domain expectations and which are best explained as innate domain-specific biases or constraints.